데이터 분석과 머신러닝에서 데이터의 분포는 모델 성능에 직접적인 영향을 미친다. 특히, 데이터가 정규 분포를 따를 때 많은 통계적 기법화 머신러닝 모델이 더 잘 작동한다. 그러나 현실의 데이터는 대체로 정규성을 띠지 않는 경우가 많다. 이를 확인하는 대표적인 지표가 왜도(Skewness)와 첨도(Kurtosis)이며, 데이터의 왜곡을 줄이기 위한 대표적인 방법이 로그변환(Log Transformation)이다. 이번 글에서는 왜도, 첨도, 로그 변환에 대해 자세히 설명하고, 실습 코드와 함께 분석 방법을 소개하겠다.
1. 왜도(Skewness)란?
1.1 왜도의 개념
왜도(Skewness)는 데이터의 비대칭성을 나타내는 지표로, 데이터 분포가 평균을 기준으로 얼마나 기울어져 있는지를 측정한다. 정규 분포라면 왜도 값이 0에 가까우며, 양수일 경우 오른쪽으로 치우친 분포(Positive Skew), 음수일 경우 왼쪽으로 치우친 분포(Negative Skew)를 나타낸다.

1.2 왜도의 공식
왜도는 다음 수식으로 계산할 수 있다.
$$S = \frac{\sum_{i=1}^{n} (x_i - \bar{x})^3 / n}{\left( \sum_{i=1}^{n} (x_i - \bar{x})^2 / n \right)^{3/2}}$$
- \(x_i\) : 개별 데이터 값
- \(\bar{x}\) : 데이터 평균
- \(n\) : 데이터 개수
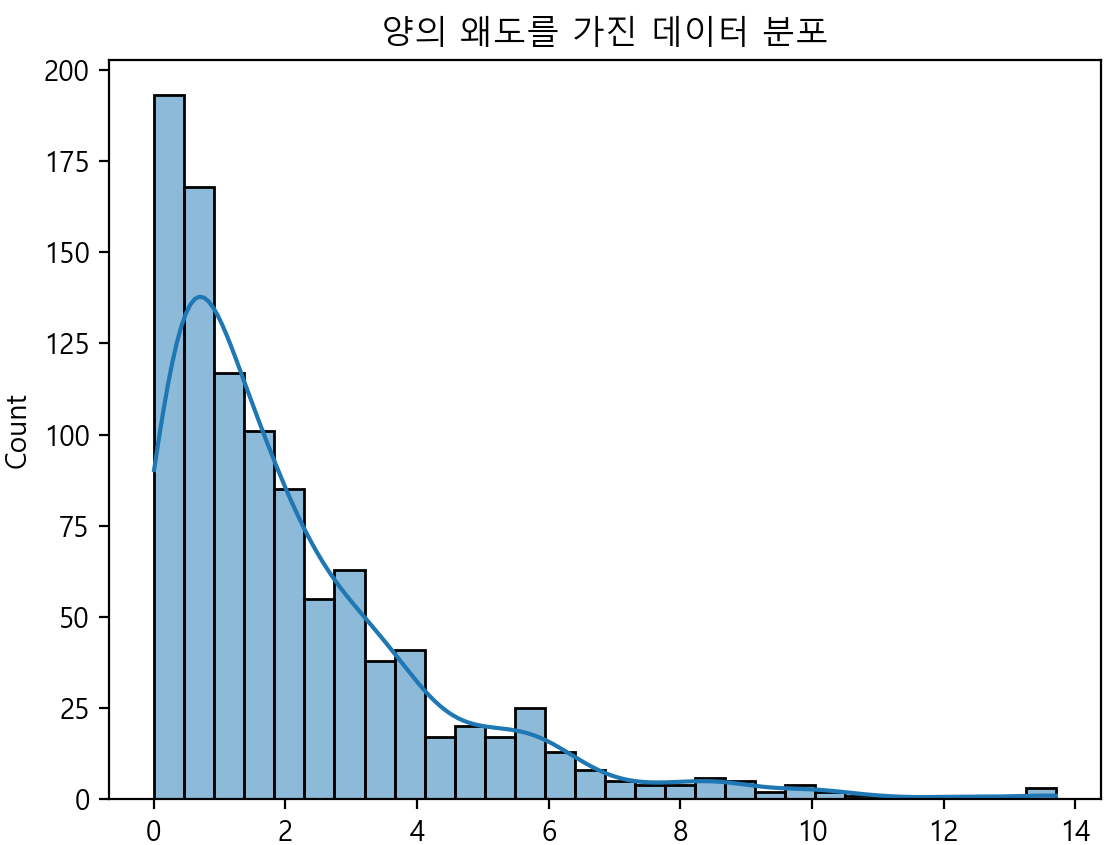
1.3 왜도의 예시 및 시각화
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import skew
plt.rcParams['font.family'] ='Malgun Gothic'
plt.rcParams['axes.unicode_minus'] =False
# 데이터 생성
data = np.random.exponential(scale=2, size=1000)
# 왜도 계산
print("왜도:", skew(data))
# 데이터 시각화
sns.histplot(data, bins=30, kde=True)
plt.title("양의 왜도를 가진 데이터 분포")
plt.show()
2. 첨도(Kurtosis)란?
2.1 첨도의 개념
첨도(Kurtosis)는 분포의 뾰족한 정도를 나타내는 지표이다. 일반적으로 정규 분포의 첨도는 3이며, 이를 기준으로 다음과 같이 분류한다.
- 첨도가 3보다 크다 (Leptokurtic, 뾰족한 분포) -> 극단적인 값이 많음
- 첨도가 3과 비슷하다 (Mesokurtic, 정규 분포에 가까움)
- 첨도가 3보다 작다 (Platykurtic, 완만한 분포) -> 극단적인 값이 적음
2.2 첨도의 공식
$$K = \frac{\sum_{i=1}^{n} (x_i - \bar{x})^4 / n}{\left( \sum_{i=1}^{n} (x_i - \bar{x})^2 / n \right)^2}$$
- \(x_i\) : 개별 데이터 값
- \(\bar{x}\) : 데이터 평균
- \(n\) : 데이터 개수
2.3 첨도의 예시 및 시각화
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import kurtosis
plt.rcParams['font.family'] ='Malgun Gothic'
plt.rcParams['axes.unicode_minus'] =False
# 데이터 생성
data = np.random.gamma(shape=5, scale=1, size=1000)
# 첨도 계산
print("첨도:", kurtosis(data, fisher=False))
# 데이터 시각화
sns.histplot(data, bins=30, kde=True)
plt.title("높은 첨도를 가진 데이터 분포")
plt.show()

3. 로그 변환(Log Transformation)
3.1 로그 변환이란?
로그 변환은 데이터의 분포를 정규 분포에 가깝게 만들기 위해 사용하는 변환 기법이다. 특히, 오른쪽으로 긴 꼬리를 가진 분포(양의 왜도)를 완화하는 데 효과적이다.
3.2 로그 변환 공식
로그 변환은 다음 공식을 따른다.
$$X' = \log(X + c)$$
- \(X\) : 원본 데이터
- \(c\) : 0이하의 값이 존재할 경우, 상수를 더해 로그 변환이 가능하도록 조정
3.3 로그 변환 적용 예제 및 시각화
import numpy as np
from scipy.stats import skew, kurtosis
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] ='Malgun Gothic'
plt.rcParams['axes.unicode_minus'] =False
# 데이터 생성
data = np.random.exponential(scale=2, size=1000)
# 로그 변환 적용
log_data = np.log1p(data)
# 변환 전 왜도 및 첨도 계산
print("로그 변환 전 왜도:", skew(data))
print("로그 변환 전 첨도:", kurtosis(data, fisher=False))
# 변환 후 왜도 및 첨도 계산
print("로그 변환 후 왜도:", skew(log_data))
print("로그 변환 후 첨도:", kurtosis(log_data, fisher=False))
# 로그 변환 전후 비교
fig, ax = plt.subplots(1, 2, figsize=(12, 5))
sns.histplot(data, bins=30, kde=True, ax=ax[0])
ax[0].set_title("로그 변환 전")
sns.histplot(log_data, bins=30, kde=True, ax=ax[1])
ax[1].set_title("로그 변환 후")
plt.show()

4. 로그 변환의 한계점과 대안
4.1 로그 변환의 한계점
- 로그 변환은 음수 및 0값을 처리할 수 없다.
- 데이터가 정규 분포를 따르도록 보장하지는 않는다.
4.2 대안적 변환 방법
1) 제곱근 변환 (Square Root Transformation)
- \(X' = \sqrt{X}\)
- 로그 변환보다 완만한 변환 효과를 가짐
2) 박스-콕스 변환 (Box-Cox Transformation)
- \(X' =
\begin{cases}
\frac{X^\lambda - 1}{\lambda}, & \text{if } \lambda \neq 0 \\
\ln(X), & \text{if } \lambda = 0
\end{cases}\) - \(\lambda\) 값에 따라 다양한 형태로 변환 가능
- SciPy의 boxcox() 함수를 사용하여 최적의 \(\lambda\) 값을 자동으로 찾을 수 있음
import numpy as np
from scipy.stats import skew, kurtosis, boxcox
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] ='Malgun Gothic'
plt.rcParams['axes.unicode_minus'] =False
# 데이터 생성
data = np.random.exponential(scale=2, size=1000)
# 변환 전 왜도 및 첨도 계산
print("변환 전 왜도:", skew(data))
print("변환 전 첨도:", kurtosis(data, fisher=False))
# 박스콕스 변환
boxcox_data, lambda_value = boxcox(data + 1) # 음수 방지
# 변환 후 왜도 및 첨도 계산
print("변환 후 왜도:", skew(boxcox_data))
print("변환 후 첨도:", kurtosis(boxcox_data, fisher=False))
# 박스콕스 변환 전후 비교
fig, ax = plt.subplots(1, 2, figsize=(12, 5))
sns.histplot(data, bins=30, kde=True, ax=ax[0])
ax[0].set_title("박스콕스 변환 전")
sns.histplot(boxcox_data, bins=30, kde=True, ax=ax[1])
ax[1].set_title("박스콕스 변환 후")
plt.show()

5. 결론 및 요약
- 왜도와 첨도는 데이터 분포의 형태를 파악하는 중요한 지표이다.
- 로그 변환을 사용하면 양의 왜도를 줄이고 정규 분포에 가깝게 만들 수 있다.
- 로그 변환이 효과적이지 않을 경우 제곱근 변환 또는 박스-콕스 변환 등의 대안을 고려할 수 있다.
데이터 분석에서는 데이터 전처리가 모델 성능에 큰 영향을 미친다. 따라서 데이터의 분포를 이해하고 적절한 변환 기법을 적용하는 것이 중요하다.
'데이터 분석' 카테고리의 다른 글
| 데이터 전처리 (Data Preprocessing) (0) | 2025.03.12 |
|---|---|
| 탐색적 데이터 분석 (EDA : Exploratory Data Analysis) (0) | 2025.03.10 |
| 범주형 데이터 처리 (0) | 2025.03.10 |
| 특징 선택(Feature Selection) (0) | 2025.03.10 |
| 표준화(Standardization)와 정규화(Normalization) (0) | 2025.03.09 |
