1. Convolution
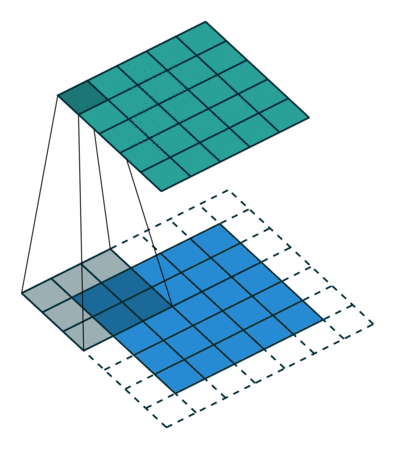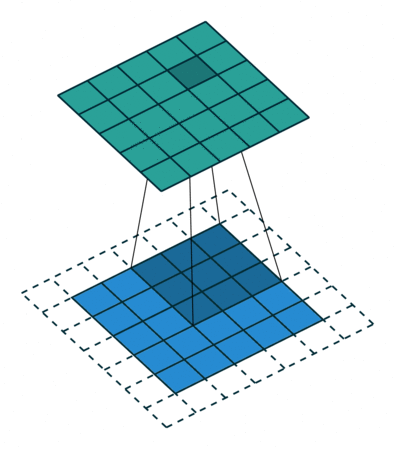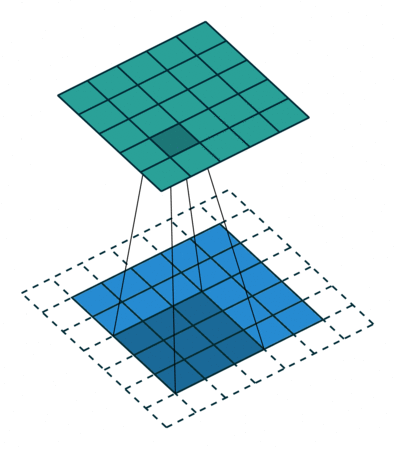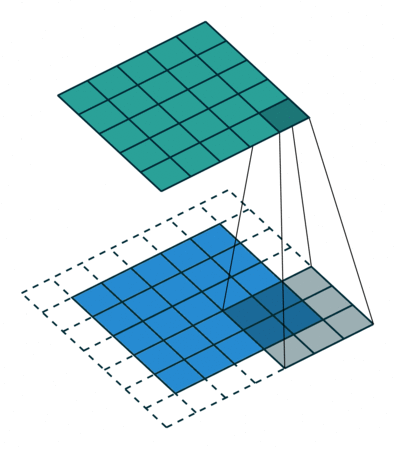
가장 기본적인 형태의 2차원(2D) 컨볼루션은 일반적으로 3x3 크기의 커널(kernel)을 사용하며, 스트라이드(stride)는 1, 패딩(padding)은 입력 차원을 유지하기 위해 사용하는 방식이다.
다양한 컨볼루션 기법을 이해하기 전에 가장 기본적인 구성 요소를 살펴보면 다음과 같다.
Kernel Size (커널 크기)
- 커널 크기는 입력 이미지에서 한 번에 처리할 영역의 크기를 결정하며, 주로 2차원 이미지에서는 3x3 픽셀 크기를 가장 많이 사용한다.
- 커널 크기가 클수록 더 넓은 영역의 특징을 고려하지만, 계산 비용도 증가하게 된다.
Stride (스트라이드)
- 스트라이드는 커널이 이미지 위를 이동할 때 한 번에 움직이는 픽셀의 수를 의미한다.
- 기본값은 1로 설정되며, 이 경우 이미지 전체를 세밀하게 스캔한다.
- 스트라이드를 2 이상으로 설정하면, Max Pooling과 유사하게 출력 이미지 크기를 다운샘플링(downsampling)할 수 있다.
Padding (패딩)
- 패딩은 입력 이미지의 가장자리에 추가로 픽셀을 채워 넣어 출력 이미지의 크기를 조절하는 방법이다.
- 패딩이 적용된 컨볼루션은 입력과 출력의 이미지 크기가 동일하게 유지되도록 한다.
- 패딩이 없는 경우 커널 크기가 1보다 클 때 출력 이미지의 크기가 점점 줄어드는 현상이 나타난다.
Input & Output Channels (입력 및 출력 채널)
- 컨볼루션 레이어는 입력 채널 수(I)를 받아 출력 채널 수(O)를 생성하는 계산을 수행한다.
- 이때 컨볼루션 레이어에서 필요한 파라미터 수는 다음 공식으로 계산할 수 있다.
$$\text{파라미터 수} = I \times O \times K^2$$
- 위 수식에서 \(K^2\)은 커널의 크기(가로 x 세로)이다.
이미지 크기 변화 (Height, Width)
- 출력 이미지 크기는 커널 크기(k), 스트라이드 크기(S), 패딩 크기(P), 입력 이미지 크기(H, W)에 따라 결정된다.
- 출력 이미지 크기를 계산하는 공식은 다음과 같다.
$$Output Height = \left\lfloor \frac{H - k + 2P}{S} \right\rfloor + 1$$
$$Output Width = \left\lfloor \frac{W - k + 2P}{S} \right\rfloor + 1$$
- 스트라이드가 클수록, 패딩이 작거나 없을수록 출력 이미지의 크기는 점점 줄어든다.
2. Dilated Convolution (Atrous Convolution)
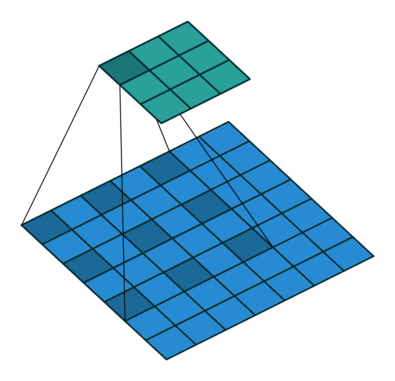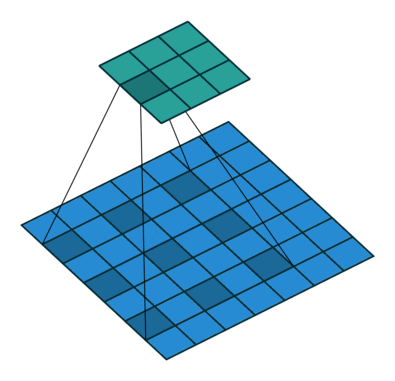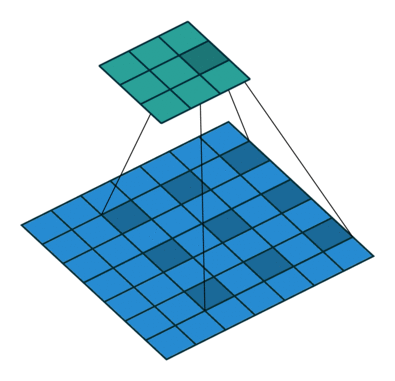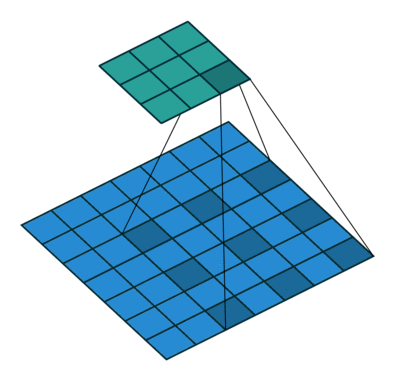
Dilated Convolution은 기존의 컨볼루션 필터에서 픽셀 간의 간격을 두어 더 넓은 수용 영역(Receptive Field)을 확보하는 방식이다. 이를 Atrous Convolution이라도 부른다.
주요 특징
- Dilation Rate(팽창률)
- Dilated convolution은 커널 픽셀 사이에 간격을 정의하며, 이 간격의 크기를 dilation rate라고 한다.
- 예를 들어, dilation rate가 2인 3x3 커널은 실제로는 5x5 크기의 수용 영역(view)을 가지지만, 사용하는 파라미터 수는 여전히 3x3인 9개로 동일하다.
- 파라미터 효율성
- 적은 파라미터 수로 더 넓은 영역을 효과적으로 살펴볼 수 있어 파라미터 효율성이 뛰어나다.
- Padding 유무
- 패딩이 없으면 출력 이미지의 크기가 줄어들지만, dilated convolution에서는 패딩 대신 간격을 벌려 더 넓은 범위를 볼 수 있게 한다.
활용 분야
- Real-time Segmentation
- 넓은 영역의 정보를 효율적으로 수집할 수 있어, 특히 실시간 세그멘테이션 분야에서 매우 유용하게 사용된다.
- Contextual Information 유지
- Pooling과 Upsampling 과정에서 발생하는 공간적 정보 손실을 방지할 수 있다. 기존 방법(Pooling -> Convolution -> Upsampling) 대비 공간적 정보를 더 잘 보존하여 해상도 손실을 최소화한다.
- Multi-Scale 대응
- dilation rate 조정을 통해 다양한 크기(Scale)의 특징(feature)을 추출할 수 있어, 여러 Scale에 대응하기 유리하다.
- Object Detection 및 Segmentation 성능 향상
- 단순히 풀링 후 업샘플링 하는 방법에 비해 Dilated Convolution을 사용하면 공간적 정보 손실을 최소화하면서 더 정확한 세부 정보와 문맥적(Contextual) 특징을 보존할 수 있다.
작동 원리
- Dilated Convolution은 필터 내부의 픽셀 사이에 빈 공간을 만들며, 실제 가중치(weight)는 제한된 픽셀에만 적용된다. 나머지 부분은 0으로 채워진다.
- 이를 통해 같은 크기의 필터로 더 큰 영역을 효과적으로 관찰할 수 있으며, 연산 비용 증가 없이 성능 향상을 기대할 수 있다.
Dilated Convolution(Atrous Convolution)은 세부적인 공간 정보를 유지하면서 넓은 영역을 파악할 수 있도록 해주며, 공간적 정보 손실을 최소화하면서도 성능을 향상시킬 수 있는 효과적인 방법이다.
3. Transposed Convolution (Deconvolution 또는 Fractionally Strided Convolution)
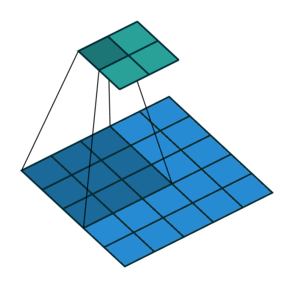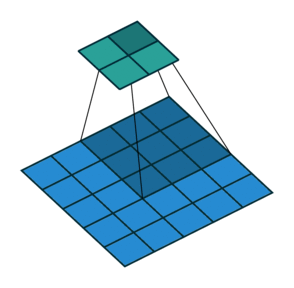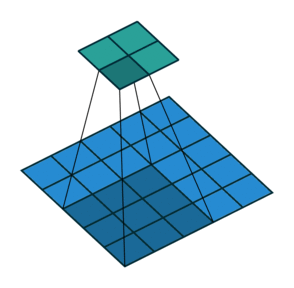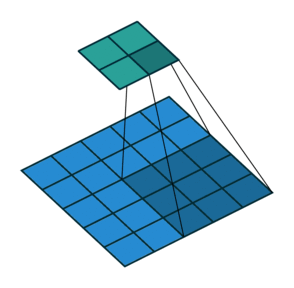
Transposed Convolution은 일반적으로 "Deconvolution"이라는 이름으로 많이 사용되지만, 실제 Deconvolution과는 다르다. 실제 Deconvolution은 컨볼루션의 연산을 역으로 수행하여 원본 입력 이미지를 복원하는 과정을 의미하는데, 이는 매우 복잡하고 잘 사용되지 않는다.
실제 Deconvolution과의 차이
- 실제 Deconvolution은 컨볼루션 과정을 수학적으로 정확히 되돌리는 역연산이다.
- 하지만 Transposed Convolution은 실제로 컨볼루션 연산의 역연산을 하는 것이 아니라, 컨볼루션을 수행하는 과정에서 축소된 정보를 다시 업샘플링(Upsampling)하여 원래 해상도로 복원하는 방식이다.
Transposed Convolution의 작동 원리
- 일반적인 컨볼루션 과정에서 생성된 압축된 정보를 Transposed Convolution을 통해 다시 업샘플링하여 원본 크기로 복원한다.
- 수학적으로는 컨볼루션 과정에서 사용하는 커널(kernel)에 대응하는 희소행렬(Sparse Matrix)을 사용하며, 이 희소행렬의 전치행렬(Transpose)을 통해 다시 더 큰 크기의 행렬을 생성하는 방식으로 구현된다.
사용 분야
Encoder-Decoder 구조 (Autoencoder)
- CNN 기반의 Encoder-Decoder 구조에서 자주 사용된다.
- Encoder에서 Pooling 등으로 이미지를 압축한 후, Decoder 단계에서 원본 이미지 크기로 복원하기 위해 사용한다.
Super Resolution (초해상도)
- 이미지의 해상도를 향상시키는 Super Resolution 분야에서도 Transposed Convolution이 널리 활용된다.
- 이는 저해상도 이미지를 고해상도로 복원하는 데 효과적이다.
다른 업샘플링 방법과의 비교
- Transposed Convolution 외에도 이미지를 업샘플링하는 다양한 방법이 있다.
- 대표적인 다른 방법으로는 보간(Interpolation)이 있으며, 특히 Bilinear Upsampling이 널리 사용된다.
- Bilinear Upsampling은 인접 픽셀의 정보를 이용하여 픽셀 값을 추정하는 방식이다.
결과적으로, Transposed Convolution은 실제 Deconvolution과는 다르지만, 해상도를 복원하거나 이미지를 확대하는 데 효과적이며, 다양한 딥러닝 구조에서 빈번히 사용되는 기술이다.
4. Separable Convolution
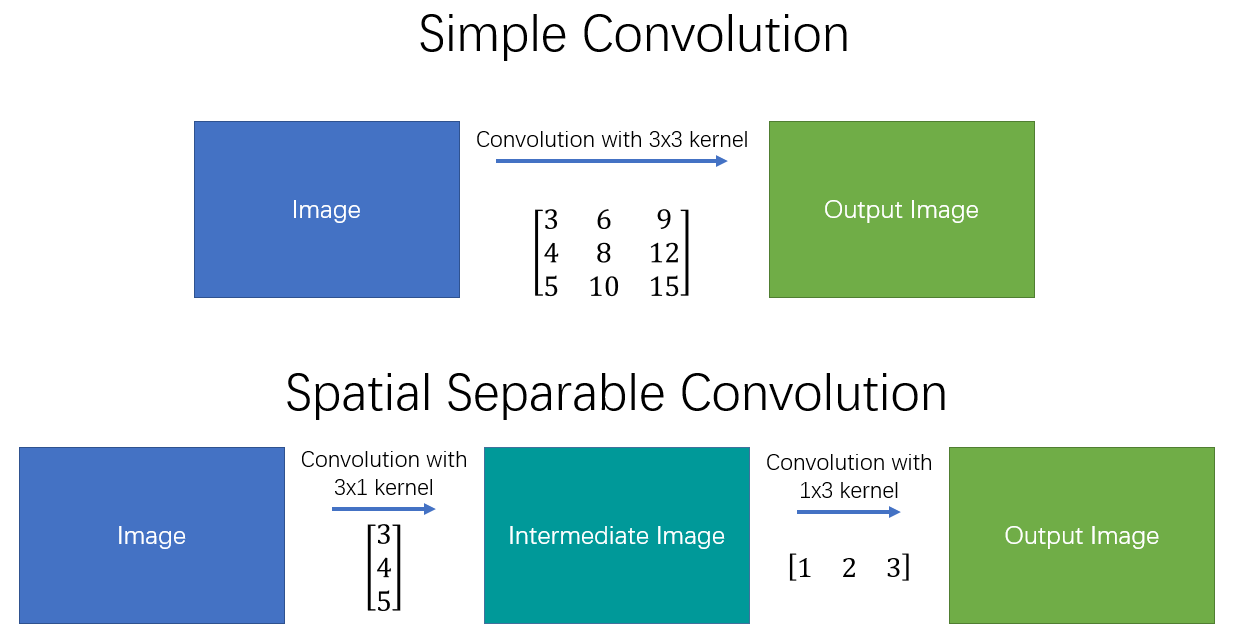
Separable Convolution은 컨볼루션 연산을 여러 단계로 나누어 계산하는 방법으로, 연산량을 크게 감소시킬 수 있다. 일반적인 컨볼루션 연산을 \(y = conv(x, k)\)로 표현할 때, x는 입력 이미지, y는 출력 이미지, k는 커널이다.
주요 개념
- 커널 \(k\)를 두 개의 더 작은 커널 \(k_1, k_2\)로 나눠서 사용할 수 있다고 가정하면, 다음과 같이 표현할 수 있다.
$$k = k_1 \cdot k_2 $$
- 이때 2D Convolution 연산을 한번 수행하는 대신 각각의 작은 커널로 1D Convolution 연산을 두 번 수행함으로써 동일한 결과를 얻을 수 있다.
연산 효율성
- 예를 들어, 원래 3x3 커널을 사용한 컨볼루션 연산은 픽셀마다 9번의 곱셈 연산이 필요하지만, Separable Convolution을 이용하면 각각의 커널로 1D Convolution을 두 번 수행하여 곱셈 연산 횟수를 줄일 수 있다.
- 이러한 방법은 계산 복잡성을 크게 낮추어 네트워크의 실행 속도를 증가시킨다.
대표적 예시: Sobel Filter
- 이미지 프로세싱에서 Sobel Mask와 같은 필터가 대표적인 Separable Convolution 예시다.
- Sobel 필터는 수평 및 수직 방향의 예지를 탐지하기 위한 필터로, Separable Convolution 방식을 통해 효율적으로 연산된다.
한계점
- Separable Convolution은 모든 형태의 커널에 적용 가능한 것은 아니다. 특정한 형태의 커널만 두 개의 작은 커널로 정확하게 분리할 수 있다.
- 따라서 사용 가능한 상황과 조건이 제한적일 수 있다는 점을 고려해야 한다.
5. Depthwise Convolution
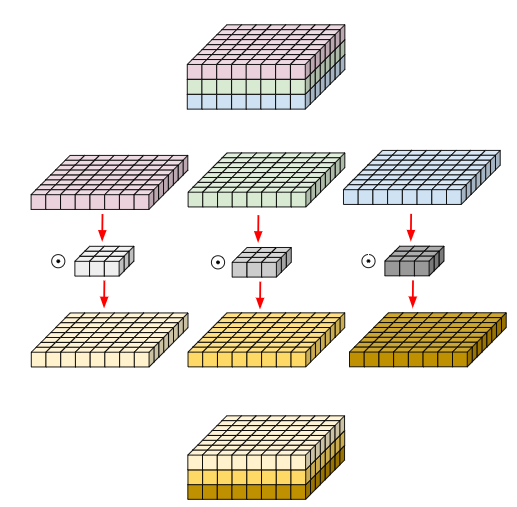
일반적인 컨볼루션 필터는 입력 영상의 모든 채널에서 정보를 통합하여 처리하므로 특정 채널의 공간적(Spatial) 특징만을 독립적으로 추출하는 것이 어렵다. 그러나 Depthwise Convolution은 각 입력 채널별로 독립된 컨볼루션을 수행하는 방식이다.
핵심 개념
- Depthwise Convolution은 입력 이미지의 각 채널에 대해 별도의 필터를 적용하여, 각 채널의 고유한 공간적 특징을 독립적으로 학습할 수 있게 한다.
- 이 방식은 채널 간 정보 통합이 없으며, 오직 공간적 방향(Spatial Direction)에서의 컨볼루션만 수행한다.
연산 방식
- 예를 들어, 8x8x3 크기의 입력 이미지에 대해 3x3x3 크기의 커널을 사용하는 경우를 생각해 보자. 이때 Depthwise Convolution은 각 8x8 크기의 채널별로 3x3 크기의 커널을 독립적으로 적용한다.
- 채널 간의 컨볼루션 연산을 수행되지 않으며, 공간적 연산만을 통해 각 채널에서 특징을 추출한다.
장점
- 연산량이 크게 감소한다. 일반적인 컨볼루션에 비해 Depthwise Convolution은 파라미터 수가 줄어들어 계산 비용이 현저히 낮아진다.
- 특히 MobileNet과 같은 효율적이고 가벼운 네트워크 구조에서 많이 사용되며, 모바일 및 실시간 환경에서 빠르게 동작할 수 있다.
Grouped Convolution과의 관계
- Depthwise Convolution은 입력 채널 수만큼 그룹을 나눈 Grouped Convolution의 특수한 형태로 볼 수 있다.
- 즉, 입력 채널의 수와 동일한 수의 그룹을 만들어, 각 그룹(채널)별로 독립적인 필터를 적용하는 방식을 의미한다.
6. Depthwise Separable Convolution
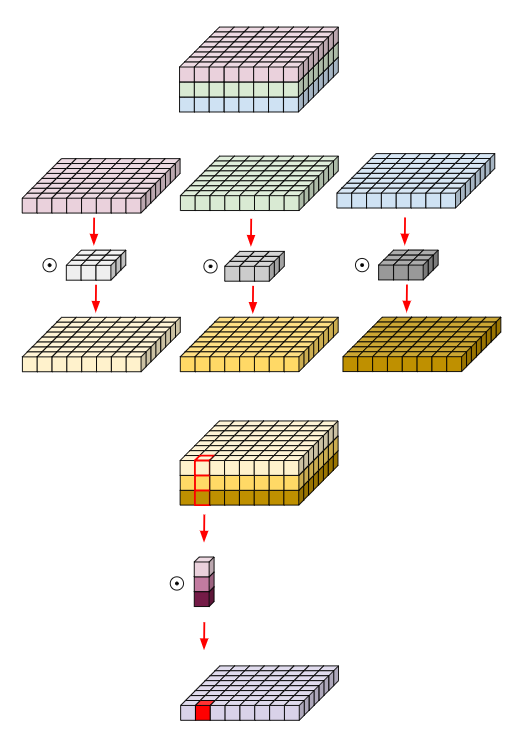
Depthwise Separable Convolution은 Depthwise Convolution과 추가적인 Pointwise Convolution(1x1 컨볼루션)을 결합하여 네트워크를 더욱 경량화하는 방법이다. 이 방법은 공간적 특징(Spatial Feature)과 채널별 특징(Channel-wise Feature)을 모두 효율적으로 추출하면서 연산량과 파라미터 수를 크게 감소시킬 수 있다.
작동 원리
- Depthwise Convolution 단계: 입력 이미지의 각 채널마다 독립적으로 공간적 특징을 추출한다. 이 단계에서는 각 채널별로 개별 필터를 사용하여, 채널 간의 정보를 혼합하지 않고 각 채널 고유의 공간적 특징만을 추출한다.
- Pointwise Convolution 단계 (1x1 Convolution): Depthwise Convolution에서 생성된 여러 채널의 결과물을 하나의 출력 채널로 압축하거나 새로운 특성 조합을 만들기 위해 수행한다. 이 단계에서는 채널 간 정보를 혼합하고 압축하여 최종적으로 채널 수를 줄이거나 조정한다.
장점
- 기존 컨볼루션 방식과 비교해 파라미터 수와 연산량이 현저히 줄어들어 효율성이 높다.
- 네트워크의 경량화를 가능하게 하여 모바일이나 실시간 처리 환경에 적합하다.
주요 활용 사례
- MobileNet과 같은 모바일 및 경량화 모델에서 매우 널리 사용된다.
- 이미지 분류, 객체 탐지, 의미론적 분할(Semantic Segmentation) 등의 다양한 분야에서 적용된다.
7. Pointwise Convolution
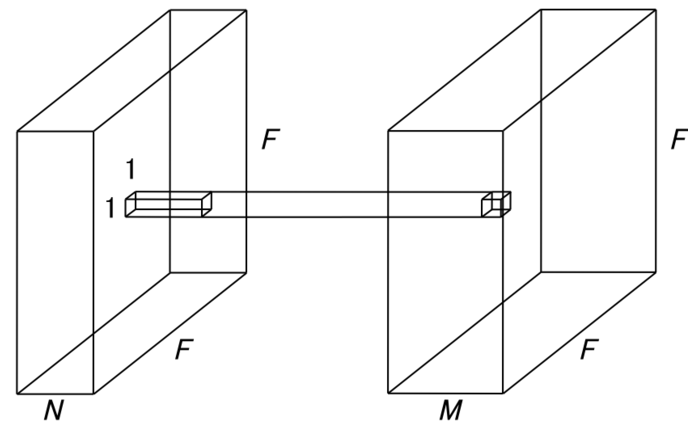
Pointwise Convolution은 공간 방향(Spatial Direction)의 컨볼루션은 수행하지 않고, 오로지 채널 방향(Channel-wise)으로만 연산을 수행하는 컨볼루션 방식이다. 주로 채널 수를 감소시키거나 특징의 차원을 축소할 때 사용된다.
작동 방식
- Pointwise Convolution은 커널 크기가 1x1로 고정된 컨볼루션 레이어이다.
- 공간적 특징(Spatial Feature)의 추출 없이, 입력 채널의 특징을 결합하거나 압축하는 연산을 수행한다.
특징
- 1x1xC 형태의 커널을 사용하여 입력 채널들 간의 선형 조합(Linear Combination)을 수행한다.
- 채널 단위의 Linear Combination을 통해 입력 채널의 수를 효율적으로 조정할 수 있다.
- 채널 수가 감소하면 다음 레이어의 계산량 및 파라미터 수를 현저히 줄일 수 있어 네트워크 경량화에 효과적이다.
장점
- 빠른 연산 속도를 확보할 수 있으며, 네트워크의 계산 비용을 크게 낮춘다.
- 채널 간 중요도를 조정하여 불필요한 정보를 희석시키고 효율적인 표현이 가능하다.
단점 및 주의점
- 데이터의 차원을 축소할 때, 일부 정보가 압축되어 소실될 가능성이 있다.
- 따라서 성능 향상과 정보 손실 사이에서의 trade-off를 신중히 고려하여야 한다.
활용 사례
- Inception, Xception, SqueezeNet, MobileNet과 같은 대표적인 경량화 네트워크 구조에서 적극적으로 활용된다.
- 이러한 모델에서는 Pointwise Convolution을 통해 성능 개선과 효율적인 계산을 동시에 달성할 수 있음이 입증되었다.
8. Grouped Convolution
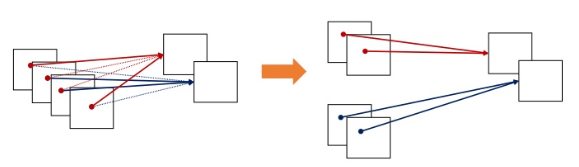
Grouped Convolution은 입력 채널을 여러 개의 그룹으로 나누어 각 그룹에 대해 독립적으로 컨볼루션 연산을 수행하는 방식이다. 이는 구현이 간단하며 병렬 처리에도 매우 유리한 기법이다.
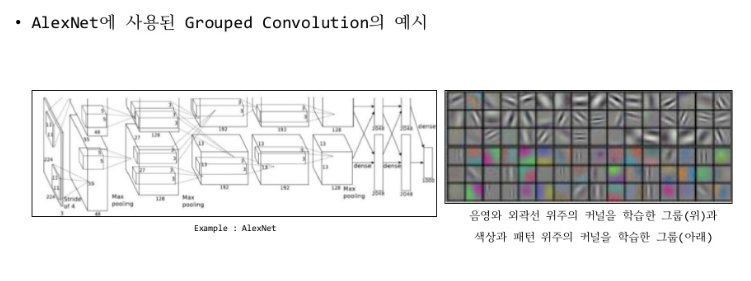
핵심 개념
- 입력 채널을 여러 개의 그룹으로 나누고, 각 그룹에서 독립적인 컨볼루션 필터를 적용한다.
- 각각의 그룹은 독립적으로 학습되어, 높은 연관성을 가진 채널끼리 효과적인 특징 추출을 수행할 수 있다.
장점
- 전체 컨볼루션보다 파라미터 수와 연산량이 현저히 줄어들어 계산 효율성을 높인다.
- 그룹 내 채널들이 서로 강한 상관관계를 가질 경우, 각 그룹이 더효과적으로 학습될 수 있다.
연산량 및 파라미터 계산
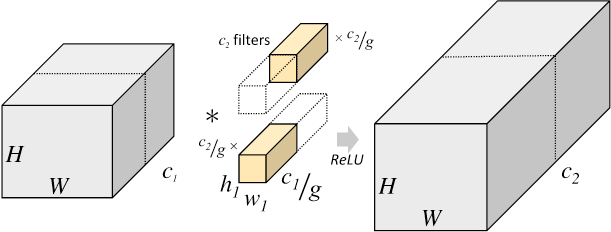
- 기존 2D Convolution:
- 필터 크기 \(K\), 입력 채널 수 \(C\), 출력 채널 수 \(M\), 입력 이미지 크기가 \(H \times W\)라면:
- 총 파라미터 수: \(K^2 \times C \times M\)
- 총 연산량: \(K^2 \times C \times M \times H \times W\)
- Grouped Convolution은 다음과 같이 연산이 축소된다.
- 한 그룹당 파라미터 수: \(K^2 \times \frac{C}{g} \times \frac{M}{g}\)
- 전체 그룹의 파라미터 수: \(\frac{K^2 \times C \times M}{g}\)
- 여기서 g는 그룹의 수이다.
그룹 수 설정의 중요성
- 그룹 수 g는 네트워크 설계 시 중요한 하이퍼파라미터이다.
- 너무 적으면 효율성 향상 효과가 미미하고, 너무 많으면 성능이 저하될 수 있으므로 적절히 선택해야 한다.
- 그룹 수가 많아질수록 독립성이 높아지지만, 너무 많으면 오히려 각 그룹의 학습 능력이 제한되어 성능이 저하될 수 있다.
9. Deformable Convolution

Deformable Convolution은 2017년 3월 논문 "Deformable Convolutional Networks"에서 제안된 기술로, 기존 CNN의 한계를 극복하기 위해 개발되었다. 이 방법은 데이터의 sampling 위치를 동적으로 변경하여 CNN의 유연성을 높이는 데 목적이 있다.
기존 CNN의 한계점
- 일반적인 CNN의 convolution, pooling 연산은 일정한 기하학적 패턴을 가정하며 수행됨
- 고정된 receptive field로 인해 다양한 크기 및 형태의 객체를 유연하게 처리하기 어려움
- Object Detection 및 Segmentation에서 효과적인 feature 추출을 위해 추가적인 수작업이 필요함
- 복잡한 geometric transformation(스케일, 회전, 종횡비 변화 등)에 대한 대응력이 부족함
Deformable Convolution의 핵심 개념
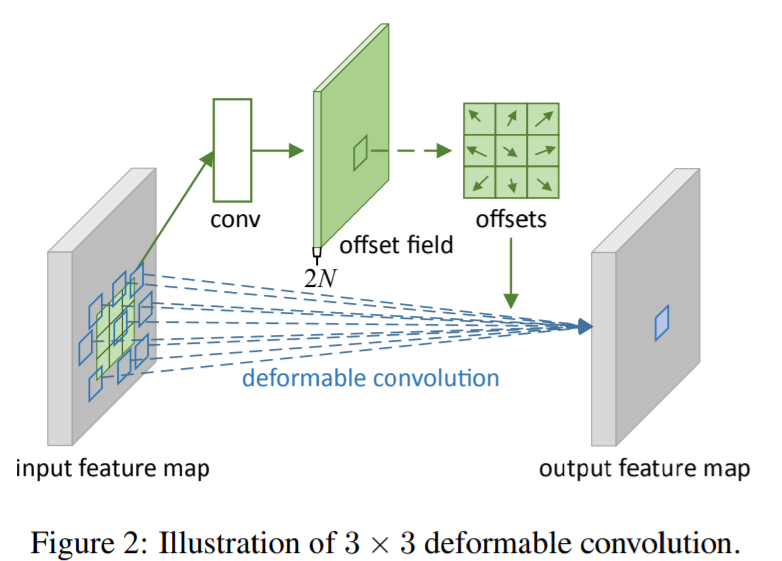
기존 CNN에서는 고정된 커널(filter)을 사용하여 feature를 추출하지만, Deformable Convolution은 기존의 정해진 sampling grid 대신, 학습 가능한 2D offset을 추가하여 데이터의 중요한 위치를 동적으로 샘플링할 수 있도록 한다. 이를 통해 CNN의 유연성을 극대화하고 다양한 변형(transformation)에 효과적으로 대응할 수 있다.
- 기존 convolution과의 차이점: 일반 CNN은 고정된 정규격의 kernel을 적용하지만, Deformable CNN은 feature의 위치에 따라 kernel의 sampling 위치가 변화할 수 있도록 구성됨
- Sampling grid 변형 가능: 스케일, 종횡비, 회전 등 다양한 형태의 변형을 학습하여 적용 가능
- 기하학적 구조 적응: 특정 물체의 형태나 크기에 맞춰 convolution kernel이 조정됨
Layer 구조 및 동작 방식
Deformable Convolution Layer는 기본적으로 두 개의 convolution 연산으로 구성된다.
- Feature Extraction을 위한 기본 Convolution Layer
- 입력 이미지에서 기본 feature map을 추출하는 역할 수행
- Offset 학습을 위한 추가 Convolution Layer
- 각 위치별로 학습된 2D offset을 기반으로 sampling 위치를 동적으로 조정
- Offset 값은 정수가 아닌 실수(fractional number)이며, bilinear interpolation을 통해 값을 보간하여 정확한 연산 수행
이러한 구조를 통해 학습 과정에서 convolution kernel과 offset을 함께 최적화하며, 입력 데이터의 특성에 맞는 적절한 sampling 위치를 자동으로 조정할 수 있다.
장점과 효과
- Receptive Field의 동적 조정: 작은 객체는 세밀하게, 큰 객체는 넓게 볼 수 있도록 receptive field를 자동 조정 가능
- 복잡한 변형 대응: 회전, 스케일 변화 등 기존 CNN이 잘 처리하지 못하는 변형에도 효과적
- Feature Extraction 성능 향상: 중요한 feature를 더욱 정교하게 추출하여 Object Detection, Segmentation 등 다양한 비전 문제에서 성능 향상
- End-to-End 학습 가능: 별도의 추가적인 preprocessing 없이 CNN 모델 내부에서 학습 가능
이러한 특성 덕분에 Deformable Convolution은 다양한 컴퓨터 비전 과제에서 성능 향상에 기여하며, 특히 객체 탐지(Object Detection)와 이미지 분할(Image Segmentation) 분야에서 널리 활용되고 있다.
